Benchmarking performance with sensitivity, specificity, precision and recall
You just finished reading the paper of the latest and greatest new bioinformatic tool. It promises to solve all your problems (maybe not all of them) and how it left every alternative tool available biting the dust. So you rush to start replacing your dull old tool with this fancy new one. But maybe, just maybe, you’re getting ahead of yourself and should probably test it out first.
It’s happened to all of us, the rush to stay on top with the newest model or fastest piece of software. The paper will have likely posted some benchmarking statistics of their own, which is the first step for us to feel confident it may work for us. But every use case is different, so it’s important to assess the performance for your own particular needs.
Benchmarking is an important process in software tool development, enabling us to quantify performance and help optimise parameters to eke out the best possible results from our tools. There are many performance metrics which we have at our disposal to assess our tools. Four popular metrics are sensitivity and specificity as well as their their closely related friends precision and recall. Often used in many papers, they can quickly give readers vital information on the performance of a test or tool, but they can sometimes be misunderstood if used in the wrong scenario. Although not shown in any of our workflow outputs, these metrics have been extensively used during their development process. In this blog post we hope to help clarify what they are showing and what to consider when benchmarking tools using one or the other.
Definitions
Many times, a tool will yield a result in a sample we feel unsure about, so how can we be confident it is correct? Before we run a multitude of samples with mysterious and unknown findings to be discovered, we want to test our tool against a dataset where we know the expected result. These expected results from an understood case are referred to as a “truth set” or “ground truth”. Using the results of our tool on this dataset and comparing them to known results, we can create a confusion matrix of all the possible outcomes (in the world of confusion matrices, this one is actually rather simple).
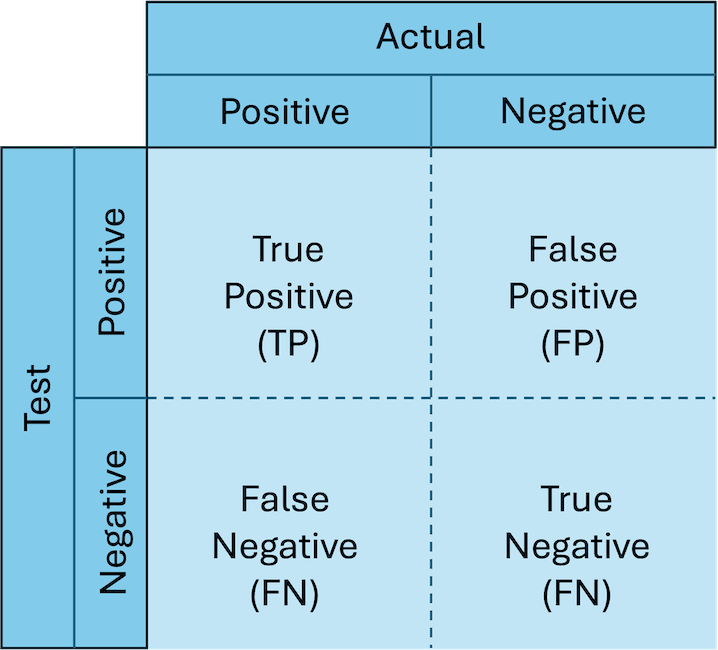
- True positive (TP) - Both the tool and the truth produced a positive result.
- True negative (TN) - Both the tool and the truth produced a negative result.
- False positive (FP) - The tool produced a positive results whilst the truth produced a negative result.
- False negative (FN) - The tool produced a negative result whilst the truth produced a positive result.
With the values within this confusion matrix, we can make the following definitions:
$$ Sensitivity = \frac{TP}{TP + FN} $$ $$ Specificity = \frac{TN}{TN + FP} $$ $$ Precision = \frac{TP}{TP + FP} $$ $$ Recall = \frac{TP}{TP + FN} $$
These can be simplified to:
- Sensitivity - Out of all the positive outcomes in the truth set, how many got a positive test result?
- Specificity - Out of all the negative outcomes in the truth set, how many got a negative test result?
- Precision - Out of all the positive test results, how many were positive in the truth set?
- Recall - Out of all the positive outcomes in the truth set, how many got a positive test result?
From these definitions, we can see sensitivity and recall are the same thing with a different name! Many other popular metrics are aliases or easily derived from these definitions, such as positive predictive value (precision), true positive rate (sensitivity or recall), true negative rate (specificity) and false positive rate (1 - specificity). In all such cases the four basic statistics are the rates of true and false, negatives and positives.
Which one to choose?
Both sensitivity and specificity, and precision and recall aim to do similar things. Depending on the type of data you have one may be more informative than the other.
The combination of sensitivity and specificity means that every state within the confusion matrix is considered. This is useful in fields such as medical diagnostics, as medical professionals need to know a negative result just as much as a positive result, so including metrics which measures the rate of true positives (sensitivity) and the rate of true negatives (specificity) makes sense.
In other examples as we shall see below, recall and precision will be preferred as the go to metrics to understand the performance of an analysis tool
When to use sensitivity and specificity
These quantities are most useful when the rates of true positives and negatives are balanced, or when the analysis should consider equally the classes.
| Truth set Positive | Truth set Negative |
|---|---|
| 100 | 100 |
Imagine we have a truth set with the above number of classifications. It has an even split of positive and negative results. We run the data through our tool and get the following results:
- TP - 86
- FN - 14
- FP - 20
- TN - 80
With this truth set, we calculate a sensitivity of 0.86 and specificity of 0.8 - not too bad. In other words, out of 100 actual positives, we correctly classified 86 (and 80 out of 100 actual negatives).
When precision and recall become useful
Above we considered a balanced dataset, one with equal numbers of true positive and negative results. But what if our truth set had a large imbalance in classifications? For example:
| Truth set Positive | Truth set Negative |
|---|---|
| 100 | 1000 |
This truth set has a much larger proportion of negative results than positive ones. For example, this could happen when screening a population for a rare disease. We run the data through our tool, compare against the known results and get the following:
- TP - 86
- FN - 14
- FP - 200
- TN - 800
In this analysis we still get a sensitivity of 0.86 and specificity of 0.8, but intuitively we can see that the results are not as good as the first. Our tool produced 286 positive calls, but 200 of these are wrong! By using sensitivity and specificity as our performance metrics we’ve obscured this glaring problem.
In this application, we don’t really care so much about the negative results, but instead want to know about the positive calls and how much we can trust them. This is where the precision-recall approach provides more insightful information: it focuses on the positive calls. You may have noticed from the above definitions, but neither precision nor recall use true negative in their calculations.
What happens if we calculate the precision and recall for the imbalanced truth set? Recall and sensitivity are the same thing so that stays at 0.86, but the precision is calculated at 0.301. The poor performance of the tool has now appeared. If a variant caller identified 286 variants in a 1100bp amplicon, but 200 of them were false alarms, you wouldn’t go near it.
Summary
In reality you are likely to use both sensitivity and specificity and precision and recall at various different stages of development.
Imbalanced binary classes are the classic case where precision and recall are used over sensitivity and specificity.
Depending on the situation and what facets of the data are most important, one pair of metrics will be more useful than the other. For many bioinformatics applications our datasets will be imbalanced, even more than in this example.
A very common example of this is that of variant calling across a genome. The number of variant sites in a genome is typically very low compared to the total size of a genome. There are therefore many many more true negative sites compared to true positives.
Example
Let’s imagine we are developing a metagenomics assay targeted at patients with inflammation in the lungs. We want to determine when this may be caused by an infection. We aim for the tool to correctly identify the presence (positive) or absence (negative) of a pathogen in a patient sample every time.
Our test can be split into 2 simple steps:
- Classify the taxa/organisms within the sample.
- Determine if there is a causative pathogen within the sample.
So the first thing we need to do is correctly classify the organisms in the sample through taxonomic classification. Taxonomic classifiers can have huge databases of information to search across and many taxa won’t be classified or present in the sample. These unclassified taxa (negatives) would take an overwhelming proportion of the data, so it will be imbalanced. Additionally we only really care about what is called by our classifier, so precision-recall seem like the right metrics to use.
Now that we have determined the microbial composition of the sample, we can determine if there is a causative pathogen present. The classifications can be well defined: either there is a pathogen present in the patient’s sample, or there is not. Our truth set here could be several patients with lung tissue inflammation, some of which are caused by pathogenic infection. The truth set should be fairly well balanced as pathogenic infection is a common cause of lung inflammation, but not the only cause. Information on the rate of true negative calls is also important, so sensitivity-specificity seems the appropriate metrics to use.
So in the development of this assay, we can use both sensitivity-specificity and precision-recall in assessing the performance.
Optimisation
As well as being useful for benchmarking the performance of the tool, both metrics can also be used to optimise parameters of an analysis. Many tools will output some form of probability, likelihood, or classification score; not a binary classification directly. In order to then transform these numbers to a binary classification we can, for examples, set a threshold cut-off value which determines the classification in a binary fashion. So-called receiver operating characteristic (ROC) curves and precision-recall curves allow us to visualise the effect of changing such threshold values. They additionally can provide a general idea on the goodness of the model’s fit.
For our metagenomics assay, we may implement an abundance threshold in which pathogens under this are not considered, as they are deemed too low to be the likely causative pathogen. An ROC curve plots true positive rate (sensitivity) against false positive rate (1-specificity) for many different threshold values. By changing the value of the threshold we can trace out a curve showing the effect the parameter.
Similarly within the taxonomic classification step we may expect a small subset of our data to be incorrectly classified. We may therefore want to apply a cut-off to exclude lowly abundant taxa from any downstream analysis. By testing a variety of different cut-offs, we can visualise their effects on performance with a precision-recall curve.
It is typical to observe a trade-off between sensitivity and specificity, or between precision and recall. This occurs naturally from the fact that algorithms are not perfect. Take a thought experiment where we randomly flip some proportion of the classifications produced by an algorithm from positive to negative, and vice-versa. The only situation in which both sensitivity and specificity will both increase is if all of these changes were from an being an incorrect classification to a correct one. (Such a situation can only occur if the algorithm is 100% incorrect - it systematically switches positive and negative classifications). It is not a stretch to see that in other situations such random perturbations can lead only to an improvement of one metric at the expense of the other. So in this sense sensitivity and specificity (and precision and recall) are anti-correlated.
Optimising for both sensitivity-specificity or precision-recall can therefore be tricky. Two derived metrics that can help in this optimisation are Youden’s J (sensitivity-specificity) and F1-score (precision-recall). These can be calculated as follows:
$$ Youden’s\ J = sensitivity + specificity - 1 $$ $$ F1-score = \frac{2\ x\ precision\ x\ recall}{precision + recall} $$
Youden’s J values range from 0 to 1, where 1 indicates a perfect prediction model and 0 indicates an even proportion of false negative and false positive calls.
Negative values can occur but indicate that the class labels have been switched.
The calculation assumes equal weighting between false positive and false negative calls, or that they are both equally important.
The F1-score value ranges from 0-1 (0-100%) and aims to maximise precision and recall.
It uses the harmonic mean of precision and recall.
The 1 in F1 indicates that precision and recall are given equal weight in this mean.
In our example metagenomics assay, for the overall test it can be argued that it’s more important to prioritise sensitivity over specificity. A false negative call results in a patient with an infection not receiving antibiotic treatment, which could have severe consequences. But a false positive call results in a patient with no infection receiving antibiotics, which is not as bad (if we disregard antimicrobial stewardship at least). The extreme end of this would be to prioritise sensitivity completely, by give everyone a positive call (i.e every patient receives antibiotics), thus eliminating any false negatives. This approach may be beneficial to patients in the short term, but there could be long term consequences such as an increase in prevalance of antimicrobal resistant pathogens. Careful consideration should be taken into priortising one metric over the other and the potential risks should be outlined clearly.
Truth sets
Regardless of the exact performance metric you decide to use, the need for a truth set when benchmarking an algorithm is paramount. The truth set can be from various sources such as:
- The current gold-standard test for whatever your assay targets, such as 16S rRNA for microbial identification or culture-based techniques.
- A reference set with known results, such as microbial standards with a defined set of organisms in a sample.
- Simulated datasets, which can be particularly helpful when there are no other appropriate sources.
Each of the above have their pros and cons, and perhaps more than one will need to be used. By using the gold standard as the truth set the benchmarking will show exactly how well your tool performs over the industry standard. But it may have known limitations such as the difficulty of delineating species with a high homology in the 16S rRNA, or the biases of growing colonies in culture. These limitations may create misleading benchmarking results such as a false positive or a false negative call with a high level of uncertainty. Reference sets such as microbial standards are good because there is little ambiguity in the truth set classification. But they may not encapsulate the challenges the test will face such as identifying species within the same genera. Simulated datasets allow you to tailor your test to the exact challenges you may come up against and you can be sure of the classification. They may not however represent the quality or composition of data you expect to encounter. The choice can be tricky: choosing one over another can result in misleading or poor benchmarking results.
For clinical applications, various regions provide programs that offer datasets for validation and benchmarking These aim to standardise procedures across multiple laboratories. A notable example is NEQAS: a UK-based organisation that welcomes participation not only from private and commercial laboratories but also from international entities, while also extending support to NHS genomics facilities.
Some commonly used truth sets we use in our work are:
Summary
Hopefully we have been able to shed some light on benchmarking metrics and our fictiously example metagenomic test has shown you where and when to use them. As a quick round-up:
- Sensitivity and specificity, and precision and recall are useful tools to benchmark performance.
- Sensitivity and specificity should be used on balanced datasets, or where a negative classification is important.
- Precision and recall are particularly useful on unbalanced datasets, for example in the detection of rare events.
- During the optimisation of sensitivity and specificity (and precision-recall), these are typically anti-correlated.
- Between applications the relative importance of the quantities may vary.
- Your choice of truth set is almost as important as your test and will influence your benchmarking results.
Happy benchmarking!
Further information
We had variant calling as an example, and luckily there’s a tool available for benchmarking already. Check out hap.py and rtg-tools for comparing variant calls against a truth set.
